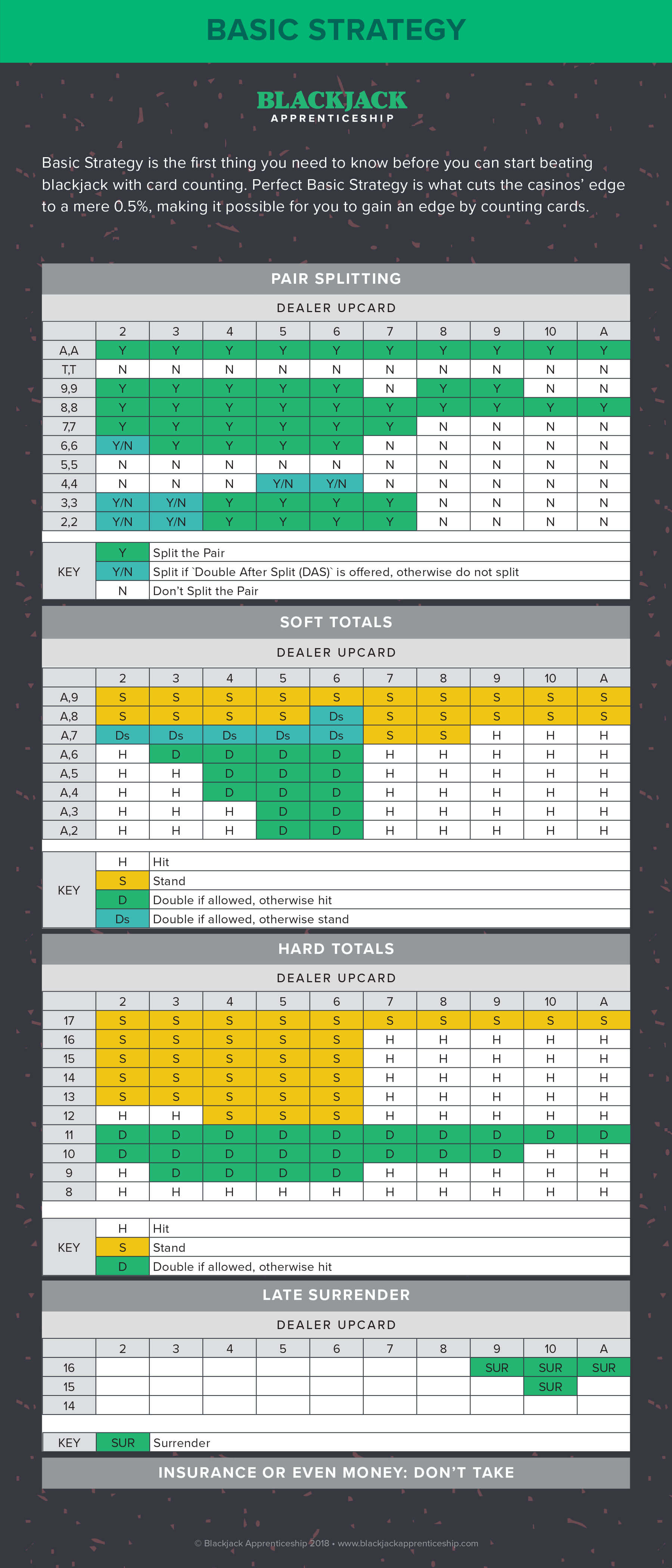
Blackjack Deviations
The standard deviation in blackjack is simply calculating the probabilities you will win or lose and extracting your odds from that. That is, the standard deviation can tell you your odds of winning, losing or pushing when playing blackjack. Blackjack should need no introduction. It is the most popular table game in the United States, and is easily found in casinos throughout the world. The object of the game of Blackjack is simply to get more points than the dealer without going over 21. Rules Hand Signals Wizard’s Simple Strategy Basic Strategy Blackjack FAQ.
Top 20 blackjack deviations At timestamp 38:42 of the same video linked above, Munchkin suggests you should get your running count accurate to 1 mistake (by a count of 1) per 3-4 shoes (about 20 decks). Blackjack deviations are those times when a player averts their attention from basic blackjack strategy to make a more advantageous play. They can also be moves made to throw off casino personnel who may suspect the player of card counting. Before you attempt to use blackjack deviations in your own play, here are some important things to know.
Deviations If this is your first visit to the Blackjack Forum, be sure to check out the FAQ by clicking the link above. You will have to r e g i s t e r (free) before you can post: click the r e g i s t e r link to proceed.
Importance of Blackjack Variances
The importance of blackjack variances and a proper understanding of variance in gambling cannot be underestimated. Blackjack players can come to think they 'know how to beat blackjack' if they go on a lucky streak, or they might come to think that blackjack isn't their game if they have a high negative variance in the early rounds of their blackjack playing. So given how important variances are to your expectations in blackjack, I'll try to explain what blackjack variance is and why it's important to keep in mind when analyzing your blackjack results.
So what are blackjack variances? To answer that question, I'll need to define a few blackjack terms -- so please bear with me.
Payout Percentages and the House Edge
The short answer is that blackjack variances are the deviations from expected payback in blackjack. 'Expected payout' is the amount of money (as a percentage) that you might expect to win back when betting on blackjack. It is closely tied to the house edge. The house edge exists so the casino stays in business, because casino games are typically weighted in the favor of the casino and against the player. The house edge in blackjack for a player using 'perfect' or optimal basic strategy is only around 0.5%, which means your expected payout will be around 99.5%.
This makes blackjack actually one of the best games in the casino. So for every $100 you bet at the blackjack table, you can expect to win back $99.50. You'll only lose $0.50 on every hundred dollars you spend (if you play perfect strategy, which all new players won't). For those managing expectations, though, the low house edge makes blackjack variances more subtle and more difficult to analyze, at least when you're going with your 'gut' or gamblers instinct.
Variances in Wins and Losses
Blackjack Deviations 18
That's because your expected payout or expectation is only an average. It's a theoretical expecation, and one not likely to occur too many times in your blackjack sessions. Sometimes you'll lose a whole lot more than $0.50 per $100 bet. You might lose $50.00 on a hundred dollar bet, if the cards aren't hitting right. On the other hand, you'll sometimes walk away from the table with more than you started out. You wouldn't play the game if you never won. So you'll win sometimes, but to account for the winning opportunities, you'll lose more than expected at other times. Losing more than you're expected to lose is a variance from your payback expectations, while winning your bets is also a variance from those expectations. Therefore, the amount your blackjack session deviates from expectation is the variance.
Blackjack Deviations
Your results will vary each time you bet on blackjack. Most of the time when playing blackjack, your results will vary widely, from large losses to large wins. Seldom will a player with a 99.5% expectation actually walk away with 99.5% of the money he or she bet. Expectation involves the odds about what you can expect to win or lose over a long period of time. Actually, it's over an infinite number of blackjack hands, because the possibility always exists that you'll just keep winning more than expected or losing more than expected.
This kind of deviation can fool a player at the blackjack table. If you're not a serious player, but just having fun, you might get the sensation you're having good luck or bad luck. You'll get the feeling you're getting lucky and that's that. Where the problem comes in is when you are a professional or serious amateur blackjack player, and you are trying out some new blackjack tips, recently learned blackjack strategy or card counting techniques. Because even really long sessions of blackjack are just a small sampling of the possibilities. Six months of blackjack sessions aren't a tiny sample, when compared to the idea that the expectation is based on a theoretical infinite number of hands. So you're not getting a full picture (or even a half-full picture) about whether your new blackjack method is working. You may just be riding the highs or lows of the blackjack variances.
So the importance of blackjack variances is they can fool us into false assumptions about our blackjack playing. Maybe you'll come away thinking you have learned how to beat blackjack, or you're a much better player than you really are. Or maybe you're doing all the right things, but the cards aren't falling your way. Players need to understand the nature of blackjack variances, then, and learn to analyze their game based not entirely on results, but on the soundness of the strategy being employed. You can make all the right moves and lose, and you can make all the wrong moves and win. That's the essence of blackjack variances. Sometimes you beat the odds.
Standard Deviation
To get an idea about our real expectations when playing blackjack, consider the standard deviation. This will give you some idea of the kind of blackjack variances you can expect. It's pretty interesting, because it shows how small the gambling margins can be in the short term, even though in the long term, blackjack is a negative expectation game.
You can figure what is called a 'standard deviation'. You might remember this from grade school, where you get an average of a group of numbers, then calculate the standard deviation from that number. In calculating a blackjack standard deviation with a computer software program, though, you won't be testing a select group of five or ten numbers. You'll be testing well over a million deviations.
The standard deviation in blackjack is simply calculating the probabilities you will win or lose and extracting your odds from that. That is, the standard deviation can tell you your odds of winning, losing or pushing when playing blackjack. Without getting too far into the numbers, at least one gambling math expert has figured there are over 723,000,000 (yes, that's 723 million) card combination scenarios where you walk away from the table a winner. But there are over 836,000,000 combinations where you walk away a loser. And there are only a paltry 144,000,000 potential cases where you walk away with the same money you started with or 'push'.
Considering all these numbers as percentages of 100%, the standard deviation will tell you that your chances of walking away a net winner in blackjack is around 42.42% of the time, rounded up. Your odds of walking away from the blackjack table a loser are around 49.10%, rounded up. Your odds of walking away with a push is somewhere around 8.47% of the time.
Blackjack Deviations From Basic Strategy
If you want to read more about the numbers behind blackjack variances and standard deviation, visit the blackjack variance page on the Wizard of Odds website. The Wizard of Odds has run statistical breakdowns of the odds on virtually every major game you'll find in a casino.
Negative Expectation, But With Hope
Blackjack Deviations Chart
So blackjack is a negative expectation game. There's a house edge that says you will lose in the long run, if you play an infinite number of hands. But in the short term, you'll walk away a winner 42% of the time. In fact, you'll walk away not losing nearly 51% of the time. And over 91% of the time, you'll experience a variance from the expected payouts in blackjack. Blackjack variances will happen 9 out of 10 times you walk up to the blackjack table. You need to keep this in mind when playing blackjack and analyzing your results.
- Appendices
- Miscellaneous
- External Links
Introduction
This appendix presents information pertinent to the standard deviation in blackjack. It assumes the player is following basic strategy in a cut card game. Each table is the product of a separate simulation of about ten billion hands played. As a reminder, the total variance playing x hands at once is the variance plus covariance × (x-1).
The following table is the product of many simulations and a lot of programming work. It shows the variance and covariance for various sets of rules.
Summary Table
| Decks | Soft 17 | Double After Split | Surrender Allowed | Re-split Aces Allowed | Expected Value | Variance | Covariance |
|---|---|---|---|---|---|---|---|
| 6 | Stand | Yes | Yes | Yes | -0.00281 | 1.303 | 0.479 |
| 6 | Stand | No | No | No | -0.00573 | 1.295 | 0.478 |
| 6 | Hit | Yes | Yes | Yes | -0.00473 | 1.312 | 0.487 |
| 6 | Hit | No | No | No | -0.00787 | 1.308 | 0.488 |
| 6 | Hit | Yes | No | No | -0.00628 | 1.346 | 0.499 |
| 6 | Hit | No | Yes | No | -0.00699 | 1.272 | 0.475 |
| 6 | Hit | No | No | Yes | -0.00717 | 1.311 | 0.488 |
| 8 | Hit | No | No | No | -0.00812 | 1.309 | 0.489 |
| 2 | Hit | Yes | No | No | -0.00398 | 1.341 | 0.495 |
By way of comparison, Stanford Wong, in his book Professional Blackjack (page 203) says the variance is 1.28 and the covariance 0.47 for his Benchmark Rules, which are six decks, dealer stands on soft 17, no double after split, no re-splitting aces, no surrender. The second row of my table shows that for the same rules I get 1.295 and 0.478 respectively, which is close enough for me.
Effect on Variance of Rule Changes
The next table shows the effect on the expected value, variance and covariance of various rule changes compared to the Wong Benchmark Rules.
Effect of Rule Variation
| Rule | Expected Value | Variance | Covariance |
|---|---|---|---|
| Stand on soft 17 | 0.00191 | -0.00838 | -0.00764 |
| Double after split allowed | 0.00159 | 0.03753 | 0.01091 |
| Surrender allowed | 0.00088 | -0.03629 | -0.01247 |
| Re-split aces allowed | 0.00070 | 0.00207 | 0.00037 |
| Eight decks | -0.00025 | 0.00071 | 0.00063 |
| Two decks | 0.00230 | -0.00530 | -0.00422 |
What follows are tables showing the probability of the net win for one to three hands under the Liberal Strip Rules, defined above.
Liberal Strip Rules — Playing One Hand at a Time
The first table shows the probability of each net outcome playing a single hand under what I call 'liberal strip rules,' which are as follows:
- Six decks
- Dealer stands on soft 17 (S17)
- Double on any first two cards (DA2)
- Double after split allowed (DAS)
- Late surrender allowed (LS)
- Re-split aces allowed (RSA)
- Player may re-split up to three times (P3X)
6 Decks S17 DA2 DAS LS RSA P3X — One Hand
| Net win | Probability | Return |
|---|---|---|
| -8 | 0.00000019 | -0.00000154 |
| -7 | 0.00000235 | -0.00001643 |
| -6 | 0.00001785 | -0.00010709 |
| -5 | 0.00008947 | -0.00044736 |
| -4 | 0.00048248 | -0.00192993 |
| -3 | 0.00207909 | -0.00623728 |
| -2 | 0.04180923 | -0.08361847 |
| -1 | 0.40171191 | -0.40171191 |
| -0.5 | 0.04470705 | -0.02235353 |
| 0 | 0.08483290 | 0.00000000 |
| 1 | 0.31697909 | 0.31697909 |
| 1.5 | 0.04529632 | 0.06794448 |
| 2 | 0.05844299 | 0.11688598 |
| 3 | 0.00259645 | 0.00778935 |
| 4 | 0.00076323 | 0.00305292 |
| 5 | 0.00014491 | 0.00072453 |
| 6 | 0.00003774 | 0.00022646 |
| 7 | 0.00000609 | 0.00004263 |
| 8 | 0.00000066 | 0.00000526 |
| Total | 1.00000000 | -0.00277282 |
The table above reflects the following:
- House edge = 0.28%
- Variance = 1.303
- Standard deviation = 1.142
Probability of Net Win
I'm frequently asked about the probability of a net win in blackjack. The following table answers that question.
Summarized Net Win in Blackjack
The next three tables break down the possible events by whether the first action was to hit, stand, or surrender; double; or split.
Net Win when Hitting, Standing, or Surrendering First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 1.5 | 77147473 | 0.05144768 | 0.07717152 |
| 1 | 537410636 | 0.35838544 | 0.35838544 |
| 0 | 127597398 | 0.08509145 | 0 |
| -0.5 | 76163623 | 0.05079158 | -0.02539579 |
| -1 | 681213441 | 0.45428386 | -0.45428386 |
| Total | 1499532571 | 1 | -0.04412269 |
Net Win when Doubling First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 2 | 89463603 | 0.54980265 | 1.09960529 |
| 0 | 11301274 | 0.06945249 | 0 |
| -2 | 61954607 | 0.38074486 | -0.76148972 |
| Total | 162719484 | 1 | 0.33811558 |
Net Win when Splitting First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 8 | 1079 | 0.00002554 | 0.00020428 |
| 7 | 10440 | 0.00024707 | 0.00172948 |
| 6 | 64099 | 0.00151694 | 0.00910166 |
| 5 | 247638 | 0.00586051 | 0.02930255 |
| 4 | 1307719 | 0.030948 | 0.123792 |
| 3 | 4437365 | 0.10501306 | 0.31503917 |
| 2 | 10222578 | 0.24192379 | 0.48384758 |
| 1 | 2822458 | 0.06679526 | 0.06679526 |
| 0 | 5621675 | 0.1330405 | 0 |
| -1 | 3520209 | 0.08330798 | -0.08330798 |
| -2 | 9425393 | 0.2230579 | -0.4461158 |
| -3 | 3559202 | 0.08423077 | -0.25269231 |
| -4 | 828010 | 0.01959538 | -0.07838153 |
| -5 | 152687 | 0.00361343 | -0.01806717 |
| -6 | 30536 | 0.00072265 | -0.00433592 |
| -7 | 3972 | 0.000094 | -0.000658 |
| -8 | 305 | 0.00000722 | -0.00005774 |
| Total | 42255365 | 1 | 0.14619552 |
Liberal Strip Rules — Playing Two Hands at a Time
The following table shows the net result playing two hands at a time under the Liberal Strip Rules, explained above. The Return column shows the net win between the two hands.
6 Decks S17 DA2 DAS LS RSA P3X — Two Hands
| Net win | Probability | Return |
|---|---|---|
| -14 | 0.00000000 | 0.00000000 |
| -13 | 0.00000000 | -0.00000001 |
| -12 | 0.00000001 | -0.00000006 |
| -11 | 0.00000003 | -0.00000035 |
| -10 | 0.00000023 | -0.00000228 |
| -9 | 0.00000163 | -0.00001464 |
| -8 | 0.00001040 | -0.00008324 |
| -7.5 | 0.00000000 | -0.00000003 |
| -7 | 0.00005327 | -0.00037288 |
| -6.5 | 0.00000009 | -0.00000061 |
| -6 | 0.00024527 | -0.00147159 |
| -5.5 | 0.00000114 | -0.00000629 |
| -5 | 0.00106847 | -0.00534234 |
| -4.5 | 0.00000967 | -0.00004352 |
| -4 | 0.00654661 | -0.02618644 |
| -3.5 | 0.00005733 | -0.00020065 |
| -3 | 0.04607814 | -0.13823442 |
| -2.5 | 0.00214887 | -0.00537218 |
| -2 | 0.23285866 | -0.46571732 |
| -1.5 | 0.03547663 | -0.05321495 |
| -1 | 0.09903321 | -0.09903321 |
| -0.5 | 0.01386072 | -0.00693036 |
| 0 | 0.14677504 | 0.00000000 |
| 0.5 | 0.05888290 | 0.02944145 |
| 1 | 0.06026238 | 0.06026238 |
| 1.5 | 0.01030563 | 0.01545845 |
| 2 | 0.17250085 | 0.34500170 |
| 2.5 | 0.03020186 | 0.07550465 |
| 3 | 0.06443204 | 0.19329612 |
| 3.5 | 0.00559850 | 0.01959474 |
| 4 | 0.01072401 | 0.04289604 |
| 4.5 | 0.00024927 | 0.00112171 |
| 5 | 0.00187139 | 0.00935695 |
| 5.5 | 0.00007341 | 0.00040373 |
| 6 | 0.00049405 | 0.00296428 |
| 6.5 | 0.00001414 | 0.00009193 |
| 7 | 0.00012404 | 0.00086825 |
| 7.5 | 0.00000369 | 0.00002767 |
| 8 | 0.00002933 | 0.00023466 |
| 8.5 | 0.00000060 | 0.00000508 |
| 9 | 0.00000543 | 0.00004888 |
| 9.5 | 0.00000007 | 0.00000063 |
| 10 | 0.00000083 | 0.00000834 |
| 11 | 0.00000013 | 0.00000141 |
| 12 | 0.00000002 | 0.00000028 |
| 13 | 0.00000000 | 0.00000005 |
| 14 | 0.00000000 | 0.00000001 |
| Total | 1.00000000 | -0.00563798 |
The table above reflects the following:
- House edge = 0.28%
- Variance per round = 3.565
- Variance per hand = 1.782
- Standard deviation per hand= 1.335
Liberal Strip Rules — Playing Three Hands at a Time
The following table shows the net result playing three hands at a time under the Liberal Strip Rules, explained above. The Return column shows the net win between the three hands.
6 Decks S17 DA2 DAS LS RSA P3X — Three Hands
| Net win | Probability | Return |
|---|---|---|
| -16 | 0.00000000 | -0.00000001 |
| -15 | 0.00000000 | -0.00000001 |
| -14 | 0.00000001 | -0.00000007 |
| -13 | 0.00000003 | -0.00000041 |
| -12 | 0.00000018 | -0.00000218 |
| -11 | 0.00000100 | -0.00001099 |
| -10.5 | 0.00000000 | 0.00000000 |
| -10 | 0.00000531 | -0.00005309 |
| -9.5 | 0.00000001 | -0.00000006 |
| -9 | 0.00002581 | -0.00023228 |
| -8.5 | 0.00000005 | -0.00000047 |
| -8 | 0.00011292 | -0.00090339 |
| -7.5 | 0.00000049 | -0.00000370 |
| -7 | 0.00046097 | -0.00322680 |
| -6.5 | 0.00000397 | -0.00002581 |
| -6 | 0.00197390 | -0.01184341 |
| -5.5 | 0.00002622 | -0.00014419 |
| -5 | 0.00969361 | -0.04846807 |
| -4.5 | 0.00022638 | -0.00101870 |
| -4 | 0.04183392 | -0.16733566 |
| -3.5 | 0.00319799 | -0.01119297 |
| -3 | 0.15826947 | -0.47480842 |
| -2.5 | 0.02641456 | -0.06603640 |
| -2 | 0.08893658 | -0.17787317 |
| -1.5 | 0.02183548 | -0.03275322 |
| -1 | 0.09681697 | -0.09681697 |
| -0.5 | 0.04992545 | -0.02496273 |
| 0 | 0.06712076 | 0.00000000 |
| 0.5 | 0.02111145 | 0.01055572 |
| 1 | 0.08978272 | 0.08978272 |
| 1.5 | 0.03789943 | 0.05684914 |
| 2 | 0.04349592 | 0.08699183 |
| 2.5 | 0.01123447 | 0.02808618 |
| 3 | 0.10813504 | 0.32440511 |
| 3.5 | 0.02489093 | 0.08711825 |
| 4 | 0.06196736 | 0.24786943 |
| 4.5 | 0.00906613 | 0.04079759 |
| 5 | 0.01805409 | 0.09027044 |
| 5.5 | 0.00154269 | 0.00848480 |
| 6 | 0.00409323 | 0.02455940 |
| 6.5 | 0.00027059 | 0.00175885 |
| 7 | 0.00107315 | 0.00751203 |
| 7.5 | 0.00007208 | 0.00054062 |
| 8 | 0.00030105 | 0.00240840 |
| 8.5 | 0.00001824 | 0.00015505 |
| 9 | 0.00008014 | 0.00072126 |
| 9.5 | 0.00000431 | 0.00004096 |
| 10 | 0.00001901 | 0.00019010 |
| 10.5 | 0.00000081 | 0.00000846 |
| 11 | 0.00000398 | 0.00004379 |
| 11.5 | 0.00000013 | 0.00000144 |
| 12 | 0.00000078 | 0.00000939 |
| 12.5 | 0.00000002 | 0.00000023 |
| 13 | 0.00000016 | 0.00000214 |
| 13.5 | 0.00000001 | 0.00000008 |
| 14 | 0.00000003 | 0.00000045 |
| 14.5 | 0.00000000 | 0.00000001 |
| 15 | 0.00000001 | 0.00000009 |
| 15.5 | 0.00000000 | 0.00000000 |
| 16 | 0.00000000 | 0.00000002 |
| 17 | 0.00000000 | 0.00000001 |
| Total | 1.00000000 | -0.00854917 |
The table above reflects the following:
- House edge = 0.285%
- Variance per round = 6.785
- Variance per hand = 2.262
- Standard deviation per hand= 1.504
Internal Links
Written by: Michael Shackleford